Number of Ordered Factorizations
Primitive computational analyses employing the ancient parameters of deficient and abundant regarding the number of ordered factorizations. PRF Brown Falls Creek, Southern Autumn of 2004
Web Publication by Mountain Man Graphics, Australia

Introduction

The following work represents a small amount of computational research concerning the nature of ordered factorizations, and specifically the number of ordered factorizations H(n) for any given n. To obtain a brief outline of the subject matter, which will be assumed in this article, please see the reference index page, and the listed resource and definition information.

The first section deals with the ability of the number of ordered factorization to account for the harmonic relationships evident in the musical Just Intonation Scale, and introduces the notion of aliquot type.

The second section examines the ancient notion of aliquot type historically (Euclid) defined by summation of the component aliquots, and notes the three separate threads of number so formalised. Abundant numbers have the sum of their divisors greater than themselves, deficient numbers have the sum of their divisors less than themselves. In the middle, with the sum of their divisors exactly equal to the number are the "Perfect Numbers".

The issue of Perfect Numbers (see above reference) and their relationship to Mersenne Primes has recently been popularised in distributed computational arrangments over the internet. For the latest in prime technology visit www.mersenne.org.

The third section introduces a new application for these ancient aliquot types. A redefinition in terms of the number of ordered factorisations (divisors) for any given number (rather than the summation of the divisors) is investigated.

That is, we define the following categories in regard to the number of ordered factorizations.
Let the number of ordered factors of n be H(n), then:

• Deficient Ordered Factorizations ... H(n) < n
  Note that this set includes the primes for which by definition H(n) = 1.

• Balanced Ordered Factorizations ... H(n) = n
  The term balanced was used in preference to "perfect".
  The first six balanced numbers are: 1, 48, 1280, 2496, 28672, 29808.
  These numbers are scant and reclusive like their cousins the Perfect Numbers. In the following analyses these are classed as abundant.

• Abundant Ordered Factorizations ... H(n) > n
  The abundant numbers are those numbers for which
  the number of ordered factors is greater than the number itself.

Based on these axiomatic definitions, an analysis of the distribution of these aliquot types is undertaken for increasingly larger samples of sets of numbers, and their corresponding number of ordered factorizations.

It is clearly established by computational rather than theoretical means, that while the major percentage of the total numbers are deficient, despite the percentage of abundant numbers dimishing to an exceedingly small fraction, the major percentage of the total number of ordered factorizations is in fact contributed by this small fraction of abundant numbers.

The scale of this abundance is very surpising at first, and requires some adjustment in thinking. This avenue of thought leads to what Ray Tomes has defined as being the mainline harmonic numbers, which are essentially the greatest of these abundant numbers in any "locality" of the number environment n.

I would be interested in any theoretical feedback and/or responses to this article. Please also send any references to any other articles or notes related to ordered factorizations.

Best wishes for now,

Pete Brown
Falls Creek
Australia
Southern Autumn of 2004

"She [nature] indicates that the principle
which she has once and for all established shall,
and must, dominate everywhere, and that everything-
harmony, mode, melody, etc.,
must be related to and be subordinated to
the generator of the major harmony, C - e - g,
and must therefore, also
be the generator of the minor harmony".

Rameau, Music, 781.3 Sh65 pg 232

The following presentation lists all numbers between 48 and 96 (first column) and shows the number of ordered factorizations (H) for each n. The data set shows informational columns as follows:
• The number N.
• The number of ordered factorizations H.
• Ratio log10(H)/log10(N)
• Whether the numeral N is a MainLine Harmonic (RT)
• The Aliquot Type of the number N (See next section).
• The simple ratio H:N
• The corresponding harmonic note on the "Just Intonation Scale"
• Components of prime factorization ...

The data set has been sorted according to the value in either of the two ratio columns. In this manner, the numbers at the top of the data set correspond to the numbers which have the greatest number of ordered factorizations for their "scale of size".

It should be clearly noted that the notes of the Just Intonation Scale are clearly reflected in this sort. In other words, the harmonic scale of music in this instance may be seen to be defined via this property - the number of ordered factorisations.

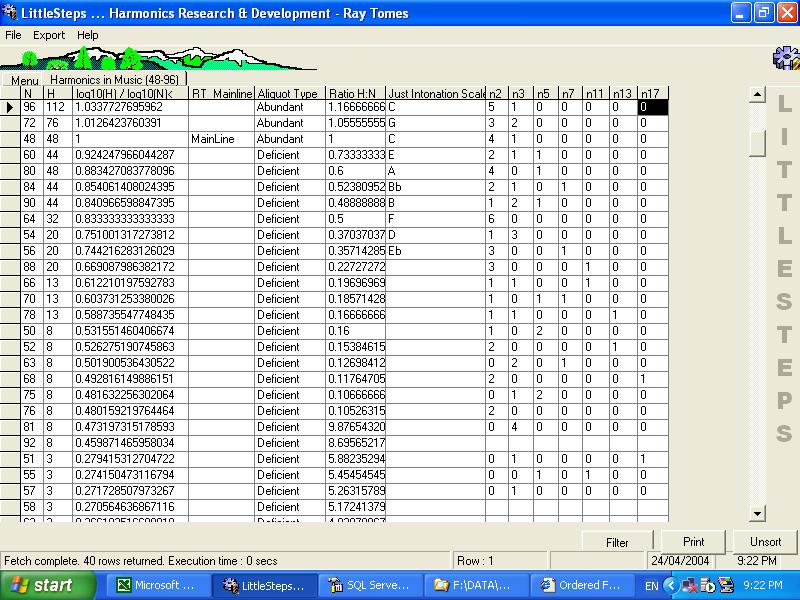
The elements of the Just Intonation Scale are related by their common factors, and their association with one another which clearly tends towards the maximisation of this number of ordered factorizations.

Aliquot is an ancient word and from it is derived the modern term quotient.
The ancient Greeks made reference to the aliquot parts
as the proper quotients of a number (not including that number).
I would not be surprised to find precedent with the ancient Indian mathematicians. Any comments, please email.

About 300BC, Euclid wrote at Proposition 36, Book 4, of The Elements,
concerning the aliquot parts and perfect numbers ...

If as many numbers as we please beginning from a unit
be set out continuously in double proportion,
until the sum of all becomes a prime,
and if the sum multiplied into the last make some number,
the product will be perfect.

About 100AD, Nichomachus elucidated this classification system for numbers:

"Among simple even numbers, some are superabundant, others are deficient:
these two classes are as two extremes opposed to one another;
as for those that occupy the middle position between the two,
they are said to be perfect.
And those which are said to be opposite to each other,
the superabundant and the deficient, are divided in their condition,
which is inequality, into the too much and the too little"

It should be clearly noted that this ancient definition continues to the present day.
This definition is based on the summation of the factors.

In the following section we propose a separate but related definition based not upon the summation,
but upon the number (ie:count) of the ordered factorizations.

AFAIK this new definition has not before been explicitly stated.
Should this not be the case, please inform the author.

Thanks.

We redefine the following categories of the numbers of ordered factorizations.
Let the number of ordered factors of n be H(n), then:
• Deficient Ordered Factorizations ... H(n) < n
  Note that this set includes the primes for which by definition H(n) = 1.

• Balanced Ordered Factorizations ... H(n) = n
  The term balanced was used in preference to "perfect".
  The first six balanced numbers are: 1, 48, 1280, 2496, 28672, 29808.

• Abundant Ordered Factorizations ... H(n) > n
  The abundant numbers are those numbers for which
  the number of ordered factors is greater than the number itself.

As can be seen in the table above, the numbers 96 and 72 are "abundant".
Where N = 96, H = 112 and where N = 72, H = 76.
These Balanced numbers have not been further distinguished in the following analyses.

As an aside, Ray Tomes has conjectured (April 2004) that the largest known balanced number is the number: 2^(2^13466918-4)*(2^13466917-1). This is a number with about 10^4053946 digits, (not 4053946 digits but 10^4053946 digits!!!), but perfectly balanced, having precisely 2^(2^13466918-4)*(2^13466917-1) ordered factorizations.

The following basic analysis consists of examination of all the numbers N and the number of ordered factorizations of n, H(n) for all n between 1 and the number 1,048,575 (or to 2^19). This dataset has been grouped by power-of-2, and the relative distribution of the above defined aliquote types are totalled for each of the increasingly expanding groups of n.

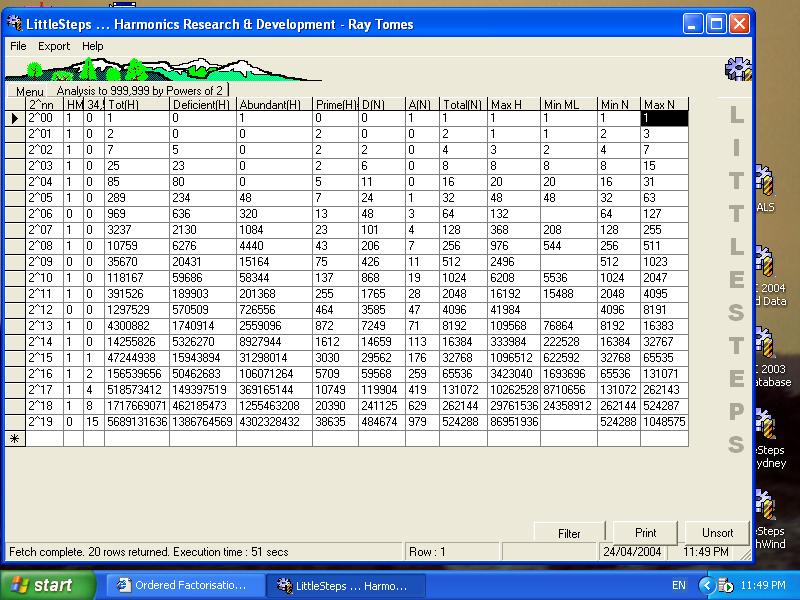
The above analysis was then somewhat extended to all n up to 16,777,216 (or to 2^23), and percentage calculation columns were added to discern the trends of relative distribution within these groups of the defined aliquot types.

Relative Distribution of Number (N)

Analysis to 16,777,216 by Powers of 2
2^nn	Prime(N)	%P(N)	D(N)	%D(N)	A(N)	%A(N)	Total(N)
2^00	0	0.0000	0	0.0000	1	100.0000	1
2^01	2	100.0000	0	0.0000	0	0.0000	2
2^02	2	50.0000	2	50.0000	0	0.0000	4
2^03	2	25.0000	6	75.0000	0	0.0000	8
2^04	5	31.2500	11	68.7500	0	0.0000	16
2^05	7	21.8750	24	75.0000	1	3.1250	32
2^06	13	20.3125	48	75.0000	3	4.6875	64
2^07	23	17.9688	101	78.9063	4	3.1250	128
2^08	43	16.7969	206	80.4688	7	2.7344	256
2^09	75	14.6484	426	83.2031	11	2.1484	512
2^10	137	13.3789	868	84.7656	19	1.8555	1,024
2^11	255	12.4512	1765	86.1816	28	1.3672	2,048
2^12	464	11.3281	3585	87.5244	47	1.1475	4,096
2^13	872	10.6445	7249	88.4888	71	0.8667	8,192
2^14	1,612	9.8389	14659	89.4714	113	0.6897	16,384
2^15	3,030	9.2468	29562	90.2161	176	0.5371	32,768
2^16	5,709	8.7112	59568	90.8936	259	0.3952	65,536
2^17	10,749	8.2008	119904	91.4795	419	0.3197	131,072
2^18	20,390	7.7782	241125	91.9819	629	0.2399	262,144
2^19	38,635	7.3690	484674	92.4442	979	0.1867	524,288
2^20	73,586	7.0177	973533	92.8433	1457	0.1390	1,048,576
2^21	140,336	6.6917	1954482	93.1970	2334	0.1113	2,097,152
2^22	268,216	6.3948	3922629	93.5228	3459	0.0825	4,194,304
2^23	513,708	6.1239	7869549	93.8123	5352	0.0638	8,388,609
Totals	1,077,871	6.4246	15683976	93.4838	15369	0.0916	16,777,216

In summary we might note that the deficient numbers (along with a dimishing number of prime numbers) dominate the first 16.777 million integers, with 99.9% of number. The percentage of the abundant ordered factorizations in this range can clearly be seen to represent only the modest percentage of 0.0916.

Relative Distribution of the number of Ordered Factorizations (H)

Analysis to 16,777,216 by Powers of 2
2^nn	Tot(H)	%D(H)	Deficient(H)	%A(H)	Abundant(H)	%P(H)	Prime(H)=P(N)
2^00	1	0.0000	0	100.0000	1	0.0000	0
2^01	2	0.0000	0	0.0000	0	100.0000	2
2^02	7	71.4286	5	0.0000	0	28.5714	2
2^03	25	92.0000	23	0.0000	0	8.0000	2
2^04	85	94.1176	80	0.0000	0	5.8824	5
2^05	289	80.9689	234	16.6090	48	2.4221	7
2^06	969	65.6347	636	33.0237	320	1.3416	13
2^07	3,237	65.8017	2,130	33.4878	1,084	0.7105	23
2^08	10,759	58.3326	6,276	41.2678	4,440	0.3997	43
2^09	35,670	57.2778	20,431	42.5119	15,164	0.2103	75
2^10	118,167	50.5099	59,686	49.3742	58,344	0.1159	137
2^11	391,526	48.5033	189,903	51.4316	201,368	0.0651	255
2^12	1,297,529	43.9689	570,509	55.9954	726,556	0.0358	464
2^13	4,300,882	40.4781	1,740,914	59.5017	2,559,096	0.0203	872
2^14	14,255,826	37.3621	5,326,270	62.6266	8,927,944	0.0113	1,612
2^15	47,244,938	33.7473	15,943,894	66.2463	31,298,014	0.0064	3,030
2^16	156,539,656	32.2364	50,462,683	67.7600	106,071,264	0.0036	5,709
2^17	518,573,412	28.8093	149,397,519	71.1886	369,165,144	0.0021	10,749
2^18	1,717,669,071	26.9077	462,185,473	73.0911	1,255,463,208	0.0012	20,390
2^19	5,689,131,636	24.3757	1,386,764,569	75.6236	4,302,328,432	0.0007	38,635
2^20	18,843,448,795	22.8560	4,306,860,069	77.1436	14,536,515,140	0.0004	73,586
2^21	62,417,265,668	20.3462	12,699,535,156	79.6536	49,717,590,176	0.0002	140,336
2^22	206,771,806,824	18.8015	38,876,235,196	81.1984	167,895,303,412	0.0001	268,216
2^23	685,060,801,921	17.0794	117,004,573,089	82.9205	568,055,715,124	0.0001	513,708
Totals	981,242,896,895	17.8304	174,959,874,745	82.1695	806,281,944,279	0.0001	1,077,871

In summary we might note that in the first 16.777 million integers
the abundant ordered factorizations are represented by only the modest percentage of 0.0916% (of numbers),
yet they account for 82.1695% of the total number of ordered factorizations.

Summary and Conclusions

The above computational results suggest that as the range of integers is extended beyond 2^23, the percentage of the abundant ordered factorizations will continue to diminish to an exceedingly small relative amount, this same small result set being responsible for the bulk percentage of the total number of ordered factorisations.

These results suggest that the ancient concept of "abundance" may be validly applied to more than the summation of factors. The new definition - by number of ordered factorizations - of deficient and abundant appears to be vindicated by the above analysis, and suggests further research might prove rewarding.

These results also support the hypotheses outlined in the Theory of Harmonics by Ray Tomes, in which critical emphasis is placed upon a defined harmonic mainline series which is represented by the most abundant of the abundant ordered factorizations.

PRF Brown
Falls Creek
Australia

Mountain Man Graphics | Index - Ordered Factorizations | Domains of Scales in the Cosmos | E-Mail